Curriculum.toen (2) – Op weg naar nationale eindtermen 1985-1990

Adri Treffers –

1. Inleiding

In 1971 stelde het project ‘Wiskunde op de basisschool’ (Wiskobas) zich ten doel een alternatief te ontwikkelen voor de formele new math waarvoor bij de Nederlandse uitgeverijen eind jaren zestig veel belangstelling bestond. Dit alternatief zou meer dan het gangbare procedurele rekenonderwijs en de new math op de realiteit en de werkelijkheid van kinderen betrokken worden, waardoor die een productieve inbreng in het onderwijs kunnen hebben.

In de periode 1971–‘81 ontwikkelde het Wiskobasteam met en in het onderwijsveld eerst een grote verzameling rijke problemen en thema’s, en vervolgens (aanzetten tot) nieuwe leergangen voor verschillende onderwerpen van rekenen, meten en meetkunde.

De publicaties van Wiskobas gingen als inspiratiebron voor enkele nieuwe methodes fungeren. Het gevolg was dat het methodebestand toen een (te) grote diversiteit ging vertonen. Dit bracht de Nederlandse Vereniging tot Ontwikkeling van het Reken-Wiskunde Onderwijs (NVORWO) ertoe om in 1984 te laten onderzoeken of en in hoeverre een nieuw reken-wiskunde programma een stevig draagvlak in het onderwijsveld zou bezitten. Dit onderzoek vond plaats op een driedaagse conferentie met 290 deelnemers, verdeeld in vier vrijwel even grote groepen van leraren basisonderwijs, begeleiders, opleiders en onderzoekers, aan de hand van een document met de belangrijkste voorgestelde veranderingen. (Cadot & Vroegindeweij, 1986; Treffers, 2015)

2. Overzicht voorgestelde wijzigingen (1984)

1. Bij de basisvaardigheden meer nadruk leggen op inzicht in het positiesysteem, hoofdrekenen, schattend rekenen en toepasbaarheid van een en ander in contextsituaties, plus een passend gebruik van de rekenmachine.

2. De aloude cijfermethodiek vervangen door een werkwijze die het cijferen leert langs de geleidelijke weg van schematisering en verkorting van kolomsgewijs rekenen, en dus niet van meet af aan op de standaardprocedures afstevent. Voor zowel het cijferend vermenigvuldigen als het staartdelen is het van groot belang dat opgaven als 7 x 265= … aan het eind van de leergang in groep 7 vlot, met direct inwisselen, uitgerekend kunnen worden.

3. Verhoudingen vanwege het grote toepassingsbereik breder opvatten dan de formele evenredigheden van het traditionele rekenen. Veel aandacht aan praktisch procentrekenen, en begrip van ‘procent’ vooropstellen.

4. Breuken en kommagetallen, en de relaties ertussen op verschillende manieren betekenis geven. De leerlingen moeten in eenvoudige probleemsituaties (benoemde) breuken en kommagetallen kunnen vergelijken, ordenen, optellen, aftrekken, vermenigvuldigen en delen. Bij een en ander speelt gelijkwaardigheid van breuken een cruciale rol; hetzelfde geldt voor de relatie tussen ‘deel-van’ en ‘keer’.

5. Aan meten, rekenen met gangbare maten en het verwerken van meetgegevens in schema’s en grafieken meer aandacht schenken en minder aandacht aan exerceren in het metrieke stelsel.

6. Meetkunde als nieuw leerstofdomein op het programma plaatsen.

Startend bij de waarnemingswerkelijkheid komen daarin vele wiskundige aspecten aan de orde, zoals het visualiseren, ruimtelijk oriënteren, projecteren, plaats bepalen, construeren, spiegelen, licht en schaduw, uitslagen van ruimtefiguren, aanzichten en bouwsels: en dat alles in samenhang met vrijwel alle onderwerpen uit de gebieden van rekenen en meten.

3. Enkele bijgevoegde voorbeeldopgaven

>1. Guus en Jack gaan de hele buitenkant van het huis schilderen.

Ze hebben zes potten verf nodig.

Iedere pot kost 16,55 gulden (euro)

Hebben ze aan 100 gulden (euro) genoeg?

>2. Mirjam is jarig op 6 november.

Die datum valt dit jaar op vrijdag.

Op welke dag is Mirjam volgend jaar jarig?

>3. Vier repen chocolade worden onder zes kinderen verdeeld.

Hoeveel krijgt één kind?

Teken verschillende manieren om vier repen met z’n zessen te verdelen en schrijf de breuken erbij.

>4. Een stok van 80 cm geeft een schaduw van 50 cm.

De schaduw van de toren is op dezelfde tijd 25 m.

Hoe hoog is de toren?

>5. Vul steeds de goede maat in (na het getal):

In onze woonkamer ligt ongeveer 24 … vloerbedekking.

De provincie Utrecht heeft een oppervlakte van 910 …

De Nederlandse postzegel heeft een oppervlakte van 525 …

De oppervlakte van je rekenboek is ongeveer 4,5 ….

>6. Kunnen dit foto’s van een en dezelfde situatie zijn?

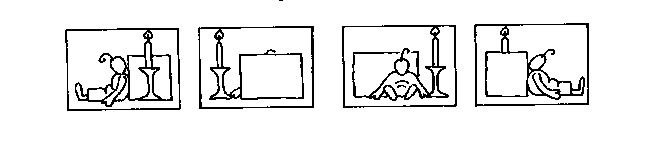
4. Veldraadpleging

De 290 respondenten konden op een vierpuntschaal (‘volledig eens – grotendeels eens – grotendeels oneens – volledig oneens’) aangeven hoe ze de beschreven onderdelen waardeerden.

Als we de gemiddelde score van 6 procent non-respons per onderdeel buiten beschouwing laten, bleek de positief instemmende score van alle genoemde onderdelen gemiddeld 97 procent te zijn.

Dit resultaat kwam op de betreffende onderdelen overeen met de uitslag van een enquête onder ouders, leraren basisonderwijs en brugklascoördinatoren. (Ahlers, 1987) Uit dit onderzoek bleek dat toegepast rekenen en hoofdrekenen belangrijker werden gevonden dan het cijferen, zij het met de aantekening dat de leraren uit het voortgezet onderwijs meer waarde aan cijferen hechtten dan de ouders en hun collega’s van het basisonderwijs. Bij ouders bleken toegepast rekenen en hoofdrekenen hoog in het vaandel te staan.

5. Proeve van een nationaal programma

De uitkomst van het opinieonderzoek was aanleiding om een ontwerp van een nieuw nationaal leerplan te ontwikkelen.

In 1989 verscheen de ‘Proeve van een nationaal programma voor het rekenwiskundeonderwijs op de basisschool. Deel 1. Overzicht einddoelen’. (Treffers, De Moor & Feijs, 1987) Vanaf 1990 ging deze publicatie als officieus leerplan en baken voor methodeschrijvers en toetsontwikkelaars fungeren. In 1993 werd de in gang gezette vernieuwing via het ‘Besluit kerndoelen basisonderwijs’ van een overheidsstempel voorzien.

De Proeve bestaat uit drie delen.

Deel A geeft een beschrijving van de algemene doelen.

Deel B bevat de concrete doelen van de leergebieden.

Deel C bestaat uit honderd voorbeeldopgaven.

Het didactische kader bestaat uit vijf ‘prins’-principes van productie, reflectie, interactie, niveau en structuur, die worden toegelicht met een thematisch voorbeeld van rekenen en meten.

De vier algemene schooldoelen hebben betrekking op:

– de persoonlijke waarde

– de voorbereidende waarde

– de maatschappelijke waarde

– de vakspecifieke waarde.

De algemene leerdoelen zijn als volgt samen te vatten.

Het onderwijs in rekenen-wiskunde is erop gericht dat leerlingen:

– een goede wiskundige werkhouding ontwikkelen

– fundamentele vaardigheden verwerven

– praktische toepassingen leren kennen

– het vaksysteem en de realiteit verbinden

– wiskundetaal begrijpen en gebruiken

– relevante verbanden, regels, patronen en structuren opsporen

– onderzoek- en redeneerstrategieën gebruiken en verwoorden

– eigen producties maken en leren reflecteren op hun aanpakken.

De ‘Proeve’ bevat 39 concrete leerdoelen, verdeeld over zes leerstofdomeinen:

– basisvaardigheden

– cijferen

– verhoudingen en procenten

– breuken en kommagetallen

– meten

– meetkunde.

De meest in het oog springende veranderingen ten opzichte van het gangbare traditionele rekenen op deze zes domeinen, sluiten aan bij wat in het voorgaande onderzoek over de kernonderdelen van een vernieuwd rekenprogramma is beschreven.

De leerdoelen worden per domein met didactische analyses, voorbeeldopgaven en inkijkjes in de klas nader toegelicht. In deel 2 ‘Basisvaardigheden en cijferen’ (Treffers & De Moor, 1990) gebeurt dit nog op uitgebreidere schaal.

Kortom het ‘wat’ en het ‘hoe’ worden bij de doelbeschrijving niet gescheiden.

6. Kerndoelen

In het eerdergenoemde OC&W rapport ‘Besluit kerndoelen basisonderwijs’ uit 1993 zijn er van de acht algemene doelen uit de Proeve slechts vijf geselecteerd, die in 1998 zelfs tot de volgende drie werden teruggebracht:

‘De leerlingen leren:

– wiskundetaal gebruiken

– praktische en formele rekenproblemen oplossen

– aanpakken te onderbouwen en te beoordelen.’

Hiermee wordt het leren problemen op te lossen als hét algemene kerndoel van het rekenonderwijs aangemerkt: kinderen moeten leren dat bij het rekenen niet alleen routinematig toepassen maar vooral ook nadenken vaak nodig is om problemen uit het leven van alledag en formele opgaven te kunnen oplossen. Dit algemene kerndoel kan uiteraard alleen gerealiseerd worden met een positieve wiskundige attitude en via de concrete leerdoelen uit de rekendomeinen waartoe de basisvaardigheden, cijferen, verhoudingen en procenten, breuken en kommagetallen, en meten en meetkunde behoren.

De concrete leerdoelen van de Proeve zijn vrijwel in z’n geheel in het ‘Besluit kerndoelen …’ overgenomen; alleen is de indeling en formulering soms wat compacter. De herziening van dit document in 1998 liet deze rekendoelen onaangetast.

Het didactische kader en de toelichting met analyses, voorbeeldopgaven en lesfragmenten van het ‘hoe’ werden niet in de kerndoelbeschrijving, het ‘wat’, opgenomen, omdat de Overheid zich daarover niet kan uitspreken – overigens een problematische kwestie, die scheiding (Biesta, 2016)

Referenties

>Ahlers, J. (1987). Grote eensgezindheid over basisonderwijs.  School, 15, 4, p. 4-10.

>Biesta, G. (2016). Een curriculum is nog geen visie. Kennisplatform voor het onderwijs.

>Cadot, J. & D. Vroegindeweij (1986). Tien voor de basisvorming rekenen-wiskunde onderzocht. Utrecht: OW & OC.

>OC&W (1993). Besluit kerndoelen basisonderwijs. ’s Gravenhage.

>Treffers, A., E. de Moor & E. Feijs (1989). Proeve van een Nationaal Programma voor het reken-wiskundeonderwijs op de basisschool. Deel 1. Overzicht einddoelen. Tilburg: Zwijsen.

>Treffers, A. & E. de Moor (1990). Proeve van een Nationaal Programma voor het reken-wiskundeonderwijs op de basisschool. Deel 2. Basisvaardigheden en Cijferen. Tilburg: Zwijsen.

adri.treffers@gmail.com