Over ontdekkend leren (2) – Probleem-oplossen met letter=cijfersommen

Adri Treffers –

Kinderen kunnen de procedure van het cijferende optellen grotendeels zelf ontdekken als een verkorting van kolomsgewijs optellen dat ze begin groep 5 hebben geleerd – en dat op zijn beurt eveneens via begeleid onderwijs is te ontdekken.

  (Huitema, 2010, 6a, p.62)

Deze stapsgewijze onderwijsaanpak van het steeds verdergaand verkorten van kolomsgewijs optellen is niet nieuw. Die werd namelijk al in de eerste complete rekenmethode in Nederland toegepast (Treffers, 2015, p.47). De gevraagde verkorting dient daarbij dan echter wel als probleem aan de leerlingen voorgelegd te worden.

Julie Menne (2019) verstopt het verkorte algoritme in een letterraadsel – een aantrekkelijke inkleding. Probleem-oplossen als middel en doel gaan op deze wijze hand in hand. Aantrekkelijk is ook dat de overgang van het oplossen van letter=cijfersommen als doel-op-zich nu makkelijk is te maken. In het volgende wordt een en ander met modelvoorbeelden toegelicht.

Neem om te beginnen twee elementaire cijfer=lettersommen.

Bij de eerste som moet worden ontdekt dat N = 0 , en dat via R een duizendtal – zeg een 1 – ingewisseld wordt. Hetgeen betekent dat E geen 1 kan zijn, want …. E = 5 is ook geen optie, … Maar bij veel andere waarden lukt het na weloverwogen puzzelen wel.

Ook bij de tweede som moet worden nagedacht, maar nu juist omdat men V + V onder de 10 dient te blijven. Wat betekent dit voor de andere letterwaarden c.q. dubbelen? De aandacht komt bij het oplossen van deze opgaven op het al dan niet inwisselen te liggen. En dat is precies waar het bij het cijferende optellen om draait. Vandaar dat de aanpak van om via zulke lettersommen het verkorte, cijferende optellen te laten ontdekken succesvol kan zijn.

Nu een modelvoorbeeld van een letter=cijfersom waarin probleem-oplossen niet primair als didactisch middel dient om de cijferprocedure te leren, maar allereerst als doel-op-zich fungeert.

De lange optelling, met tien letters en één oplossing. is een voorbeeld van onderzoekend rekenen binnen een interactieve onderwijssetting. (Nelissen, 2000) Zelfstandig probleem-oplossen is hier geen passende onderwijsvorm. Daarvoor is de opgave te lastig. Uitleggen hoe je het vraagstuk moet oplossen evenmin. Want dan schieten we het hogere cognitieve doel ervan voorbij.

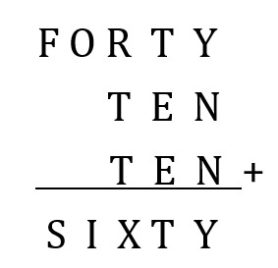
De les. Bij de introductie vertelt de leraar dat we met elkaar de beroemdste optelsom proberen op te lossen. Iets wat maar weinigen is gelukt. De belangstelling dient te worden opgewekt, de spanning opgevoerd …

1. In de korte oriëntatiefase werken de kinderen in groepjes van twee aan de letter=cijfersom die eerst wordt vertaald en verklaard.
2. Daarna wordt klassikaal geïnventariseerd wat is opgevallen: de N en de E komen in beeld, ofwel de 0 en Waarom kan N geen 5 zijn? Waarop zullen we we ons in de volgende fase van zelfstandig werken gaan richten? Waarom op de linkerkant, wat is daar zo opmerkelijk? Dit zijn zo de kwesties die in de eerste tussenbespreking aan de orde kunnen komen.
3. Nu stuit de groep op het cruciale FO-SI Of positief gesteld: hier ligt de mogelijkheid van een AHA-ervaring. Omdat de letters verschillen, zal er twee keer ingewisseld moeten worden – zo luidt de beslissende ontdekking. En dat kan alleen maar indien op de plaats van de O een 9 komt met daarboven een gedachte 1 of 2. Maar wacht, 8 zou ook kunnen. Hoewel …?
4. De tweede tussenbespreking concentreert zich op deze twee mogelijkheden. Beslissend is het argument dat 8 met 2 een 0 Maar omdat die al bezet is, moet 8 hier afvallen, en resteert 9 met daarboven een ingewisselde 2. Op de plaats van de letters O en I komen dus respectievelijk een 9 en een 1.
5. In de derde werkfase verschuift de aandacht naar de middelste kolom, waarvan de optelling boven de 20 moet uitkomen. Weer duiken twee mogelijkheden op. Beide worden uitgeprobeerd. Eén ervan moet afvallen …
6. In de laatste nabespreking lichten enkele groepjes toe waarom dat het geval moet zijn.
7. Met de bespiegelende terugblik op het oplossingsproces wordt het lesuur afgesloten.

Indien men niet eerst zelf het optelprobleem heeft opgelost, zal de lezer gemerkt hebben dat de bovenstaande bespreking moeilijk was te volgen. Exact het bezwaar dat tegen de onderwijstheorie van ‘voordoen-navolgen’ valt in te brengen. Heeft men het probleem echter wel eerst zelf aangepakt, dan zou het kunnen dat men zich meteen op de linker kolommen heeft gericht, en daardoor later het een en ander heeft moeten corrigeren. Of anders gezegd: er is niet een bepaald pad dat bij het oplossen gevolgd moet worden. Wederom een bezwaar dat tegen de eerdergenoemde CLT met zijn strak uitgewerkte voorbeeldopgaven en stappenplannen ingebracht kan worden.

Terug naar de leerstellige uitspraak van Kirschner (2018) over de beperkte denkkracht van kinderen, die essentieel van het denkvermogen van de geschoolde expert zou verschillen. Zien we dat bij dit modelvoorbeeld terug? Nee, dat is niet het geval. Hooguit is er sprake van een gradueel verschil met de wijze waarop de leraren een dergelijk probleem in een nascholingscursus oplossen.

Voor de leerlingen die plezier in dergelijke opgaven hebben nog een klassieker.

Eigen producties. De letter=cijfersommen zijn, algemeen gesproken, te lastig om eigen producties te maken. Maar zet men stippen in plaatst van letters dan zijn er mogelijkheden te over. Een voorbeeld:

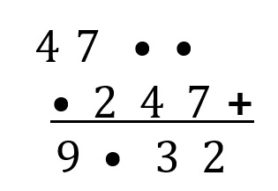
Enkele stip-voorbeelden die kinderen bedacht hebben kunnen aan de groep worden voorgelegd. De structuur van het algoritme wordt bij het samenstellen van dergelijke opgaven gedetailleerd doordacht.

Referenties

Kirschner, P. A., L. Claessens & S. Raaijmakers ( 2018). Op de schouders van reuzen. Meppel, Ten Brink.

Huitema, S. et al (2010). Wereld in getallen. Den Bosch, Malmberg.

Menne, J. (2019). Rekenspellenboek groep 5&6. Baarn, Menne Instituut.

Nelissen, J. (2000). Een pleidooi voor het interactief leren in het reken-wiskundeonderwijs. Panama Post, 19, 1, 6-14.

Treffers, A. (2015). Weg van het cijferen. Rekenmethodes vanaf 1800 tot heden. Utrecht, Freudenthal Group. reni.casoli@gmail.com.

adri.treffers@gmail.com