Blog
Handig en schattend rekenen – Getal & Ruimte junior
Adri Treffers –
1. Inleiding
Onder traditioneel rekenonderwijs verstaat de wiskundige Jan van de Craats de methodiek waarbij de leraar één efficiënte oplossingsmethode bij een bepaald type opgave aanbiedt en uitlegt, en die vervolgens laat inoefenen. Tijdens dat oefenen is er geen plaats voor contextopgaven, want die leiden alleen maar af. Nadat het rekenrecept wordt beheerst, is er wel ruimte voor contextopgaven als ‘toepassingen-achteraf’. Aan gevarieerd, handig (hoofd)rekenen dient geen speciale aandacht besteed te worden. In 2007 pleitte hij voor een terugkeer naar dit traditionele rekenen, ‘de methode van opa’.
Zijn vijf hoofdpunten vat hij als volgt samen:
‘ . 1 Herstel systematisch oefenen in ere.
. 2 Eén methode per bewerking (de methode van opa)!
. 3 Doe ‘handig rekenen’ de deur uit.
. 4 Verbied kolomsgewijs rekenen!
. 5 … en noem cijferen weer gewoon rekenen.’ [1, p.3]
Het basisprincipe van één voorgeschreven oplossingsmethode die Marcel Schmeier aan het traditionele rekenonderwijs toekent en die hij ook voor het rekenonderwijs-van-nu als leidraad wil nemen, ligt in dezelfde lijn, namelijk die van het receptmatige rekenen.
‘Nieuwe leerstof wordt uitgelegd en voorgedaan door de leerkracht, terwijl de leerlingen meeschrijven. (…) Voor iedere bewerking wordt één oplossingsprocedure aangeleerd die vervolgens wordt ingeslepen tijdens de fase van begeleide inoefening.’ [4, p.14]
Stel, die opa was in 2007 een jaar of zeventig, dan is de kans groot dat hij op school les met Fundamenteel Rekenen had gekregen, de meest gebruikte methode in die tijd. Of als hij wat jonger was, dan mogelijk Functioneel Rekenen.1) In beide gevallen een traditionele methode die niet aan de vijf geboden voldoet.
Het traditionele rekenonderwijs was altijd al een driestromenland.
De eerste stroming, internationaal als de procedurele aangeduid, voldoet aan de door hen genoemde richtlijnen, Ze hanteert eensporig uitgewerkte opgaven als leidraad voor gestandaardiseerd rekenen. De tweede stroming, de conceptuele, volgt de genoemde voorschriften niet op. Ze stimuleert leerlingen juist tot tweesporig rekenen – receptmatig en gevarieerd. De derde stroming, de duale, neemt afhankelijk van welk rekendomein, een tussenpositie in.*)
De conceptuele methodes – traditioneel en modern – scoorden in 1997 beduidend hoger dan hun procedurele tegenpolen. Individuele peilingen uit 1987 en 2004 bevestigen deze uitkomsten. Ze laten zien dat de betreffende leerlingen hoger scoren in inzichtelijk i.c. handig en schattend rekenen – twee van de tien kerndoelen van het reken – en wiskundeonderwijs op de basisschool.
Na het leren van de tafels in de onderbouw [6] stappen we hier over naar de middenbouw en gaan onderzoeken hoe deze twee rekendomeinen in de nieuwe methode Getal & Ruimte jr behandeld worden.
Maar eerst volgt de historische schets van die onderwerpen.
2. Historische context
Nieuw Rekenen (1969) is de laatste traditioneel-conceptuele methode uit de vorige eeuw. Getalinzicht, flexibel rekenen en schattend rekenen krijgen daarin een centrale plaats. Voorbeelden voor groep 6 laten zien hoe dit basisconcept daarin concreet gestalte krijgt.

Naast hoofdrekenen en schatten besteedt deze methode ook de nodige aandacht aan cijferen. De schrijvers voegen daar echter wel meteen aan toe: ‘Inzichtelijk rekenen, samen met levensecht rekenen zijn evenwel uitgangspunt en doel’.
In Naar Zelfstandig Rekenen, de grootste traditioneel-procedurele methode uit de periode 1955-1990, zal men geen enkel van deze zes somtypen aantreffen. Deze gezichtsbepalende procedurele methode voldoet aan het basisprincipe van één standaardprocedure: ze is eensporig en werkt zo snel mogelijk naar één efficiënte methode toe om een bepaald type som op te lossen. Toepassingen komen pas aan het eind van de leergang aan bod, en dan nog slechts in bescheiden mate. Handig, flexibel rekenen en schattend rekenen staan niet op het programma.
Niet verwonderlijk dat deze procedurele methode in 1997 op deze drie belangrijke onderdelen van de kerndoelen ongeveer 10 procentpunten lager scoorde dan de conceptuele Nieuw Rekenen.
Een verschil tussen de toenmalige procedurele en conceptuele methodes dat destijds bij de volgende moeilijke hoofdrekenopgaven – 12 seconden bedenktijd – met tientallen procenten opliep!

Let wel, het gaat hierbij, zoals gezegd, om twee van de tien nationale kerndoelen voor het reken-wiskundeonderwijs.
3. Een voorbeeldige les
De volgende opgave dient om de kenmerken van een conceptuele, interactief geleide rekenles weer te geven zoals die bij een moderne methode van na 2000 in praktijk gebracht worden.

Leerlingen van groep 6/7 gaan na een korte voorbespreking individueel met de brodensom aan de slag. De verschillende rekenwijzen worden door de leerlingen, en waar nodig door de leraar, met elkaar in verband gebracht De variatie aan bewerkingen biedt prachtige aangrijpingspunten om de relaties tussen de verschillende berekeningen te laten zien en vooral om de handigste aanpakken klassikaal aan de orde te stellen.
Bij a), b) en c) gaat het bij vermenigvuldigen om een reflectie op het verkorten van de rekenwijzen naar de standaardprocedure, en bij het aftrekken om de relatie tussen ‘eraf halen’ en de zogenoemde winkelmethode van ‘aanvullend optellen’. Ook de fout van 7,98 krijgt de aandacht: bij ieder brood kom je 2 cent tekort, dus bij 4 broden… De kwestie van het afronden op een stuiver komt eveneens aan bod.

Aan het eind van de les is iedereen het erover eens dat e) de beste manier bij vermenigvuldigen is, en de winkelmethode het handigste bij het aftrekken.
Algemeen geldt dat leerlingen aan het einde van groep 8 in principe alle genoemde strategieën van flexibel hoofdrekenen, schattend rekenen, kolomsgewijs rekenen en cijferen dienen te beheersen en in praktische situaties moeten kunnen toepassen. De brodensom zou globaal rekenend opgelost dienen te worden en niet (hoofd)cijferend. Maar in een andere opgave zouden de leerlingen 4 x 198 ook cijferend moeten kunnen berekenen, bijvoorbeeld als deelproduct van een grote vermenigvuldiging.
In de conceptuele methodes komt ook de volgende variant van zo’n brodensom voor.

De les zal dan ongeveer hetzelfde verlopen. Maar dan zijn er altijd wel leerlingen die de volgende oplossingen bedenken: ‘Ja, dat is genoeg, want met een tientje kan ze zelfs 4 broden van €2,50 kopen’, of
‘Ja, 5 broden kan ook, want 5 x 2= 10 …’
4. Getal en Ruimte junior
De vraag is of en hoe deze twee somtypes in Getal en Ruimte junior worden behandeld. In deel 6a staat eenzelfde opgave: 3 x 298 = …
Eerst maken de leerlingen een schatting.
En dan volgt de Uitleg van cijferend vermenigvuldigen.
Na Samen volgt Zelf waarin hetzelfde gebeurt met 4×123; 3×212; 3×324; 2×423; 3×132; en 4×131. De schattingen bij deze opgaven zijn volgens de opgegeven oplossingsregel in Samen (7×423=7×400 =2800) achtereenvolgens: 400; 600; 900; 800; 300 en 400. En bij 4×450 zou cijferend ongeveer 2000 uit de bus moeten komen, of 1600 … (!)
De eerste opgaven van schattend rekenen die de leerlingen, los van handig rekenen, krijgen aangeboden moeten volgens het antwoordenboekje als volgt worden opgelost:
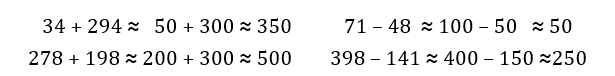
Verwarring ten top: 71 – 48 ≈ 100 – 50 ≈ 50
Terwijl dit toch betrekkelijk eenvoudige hoofdrekenopgaven zijn waarvan de bron, als het goed is, in groep 4 ontspringt.
Voor schatten geldt algemeen dat het uitsluitend dienst doet als controle van de cijferende berekening of die met de rekenmachine.
Hoe staat het met handig (hoofd)rekenen?
Het antwoord op deze vraag luidt dat dit kerndoel volledig ontbreekt.
Hoe een en ander bij aftrekken uitpakt, toont het volgende voorbeeld.

Het voorbeeld wordt in stap 3 nota bene cijferend uitgerekend (7a):
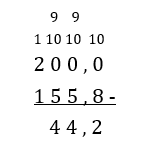
Stap 4 geeft de natuurlijke rekenwijze van aanvullend optellen in deze context weer, net zoals de winkelmethode in brodensom (1).
Deze vorm van handig rekenen ontbreekt echter al bij het aftrekken in de onderbouw waar het handige rekenen zijn oorsprong zou moeten vinden.
5. Conclusie
De slotsom kan geen andere zijn dan dat Getal & Ruimte jr op de kerndomeinen van handig en schattend rekenen al vanaf de onderbouw tekortschiet. En dat de gevolgen van dit gemis ten aanzien van de algemene uitgangspunten betreffende de persoonlijke, de voorbereidende, de wiskundige en de praktische waarden van het reken-wiskundeonderwijs ook in de leeropbrengsten van deze methode zichtbaar zullen worden.
*) Zie voor literatuurverwijzingen naar traditionele methodes en Cito-peilingen: [5]. Ook de onderzoeksresultaten van de peilingen staan in [5].
Literatuur
1). Craats, J. van (2008). Waarom Daan en Sanne niet kunnen rekenen.
Mythen in de rekendidactiek. In: Braams, T, & M. Milikowski (red.)
De gelukkige rekenklas. (p.25-37). Amsterdam: Boom.
2). Getal & Ruimte junior. (2017). Groningen: Noordhoff.
3). Huitema, S., e.a. (2001). De Wereld in Getallen. Den Bosch: Malmberg
4). Schmeier, M.(2018). Leren van uitgewerkte voorbeelden bij rekenen.
Tijdschrift voor Remedial Teaching, 3, p.24-26.
5). Treffers, A. (2015). Weg van het cijferen. Rekenmethodes vanaf 1800 tot heden. Freudenthal Group, Universiteit Utrecht. reni.casoli@gmail.com
6). Treffers, A. ( 2020). Oude tafels in een nieuwe methode. Elementair vermenigvuldigen in Getal & Ruimte junior. Volgens Bartjens, 3, p. 25-28.
adri.treffers@gmail.com


