Curriculum.toen (3) – De stille rekenrevolutie 1990-2010

Adri Treffers –

1. Inleiding

Vanaf 1990 vindt een spectaculaire verschuiving op de methodemarkt plaats. In tien jaar groeit het aandeel van de realistische methodes van twintig naar honderd procent. In het tijdvak 1990-2000 zijn tien methodes uit verschillende rekenrichtingen in gebruik. Vijf ervan, alle realistisch, verschijnen na 2000 in een euro-versie. Slechts twee methodes bestrijken de totale periode van 1990 tot 2010, te weten instructief-realistische ‘Wereld in Getallen’ (WiG) en constructief-realistische ‘Pluspunt’ (PP) Samen bedienen ze vanaf de jaren negentig ongeveer 70 procent van de scholen. Ten eerste verschillen deze moderne methodes in de organisatievorm van het onderwijs: WiG besteedt vier lessen per week (gedeeltelijk) aan klassikale instructie, en PP slechts twee. Anders gezegd: WiG doet meer recht aan het interactie-principe van het realistische reken-wiskundeonderwijs. Ten tweede, wat de inhoud betreft, stuurt WiG de leerlingen doelgerichter op de algoritmen en rekenregels af dan PP, die de teugels vaak met vrije opdrachten als ‘doe het op jouw manier’ laat vieren. Dit zijn twee redenen om het onderscheid ‘instructief’ en ‘constructief’ aan de genoemde realistische methodes te verbinden. Beide methodes schenken veel aandacht aan hoofdrekenen en schatten. Toepassingen staan bij PP vanaf het aanvangsonderwijs in een aansprekend thematisch verband; bij WiG gebeurt dit vanaf groep 6.

2. Klassikale peilingen van 1987 en 2011

Vergelijking van de resultaten uit 1987 toen 65 procent van de scholen nog een procedurele methode gebruikte, met die van 2011 toen 100 procent een conceptuele, realistische methode had ingevoerd, levert de volgende verschuivingen op.

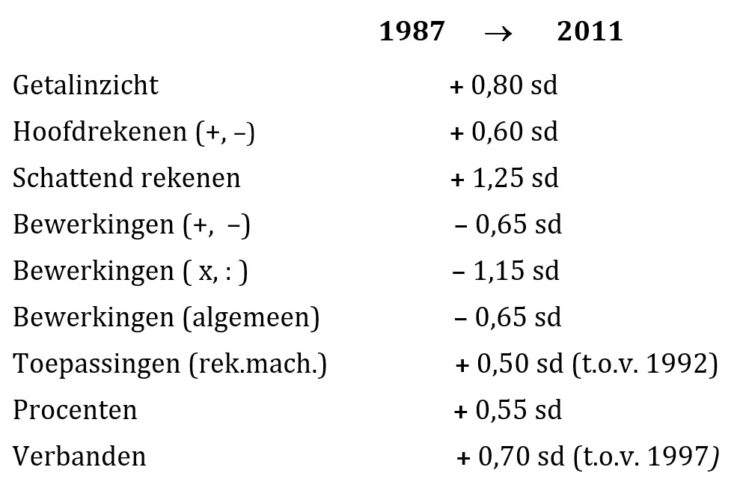
Van de 21 onderwerpen uit de rubrieken rekenen, meten en meetkunde geven we alleen de vergelijkende scores indien de verschillen meer dan 0,5 standaarddeviatie bedragen.

De opbrengst van het domein getalinzicht blijkt 0,80 sd groter te zijn. Hoofdrekenen (+,-) neemt met 0,60 sd toe, en schattend rekenen met 1,25 sd – een middelgrote tot grote stijging bij deze onderwerpen van zo’n 10 tot 25 procentpunten. Slechts bij hoofdrekenen (x,:) bestaat er nagenoeg geen verschil. De goedscores van het cijferen nemen af.

De scores bij verhoudingen en breuken zijn slechts gering in positieve zin veranderd. Dit in tegenstelling tot die van procenten, waar de goedscore wel aanzienlijk is toegenomen.

Alleen bij ‘toepassingen m.b.v. de rekenmachine’ en bij ‘tabellen, grafieken en verbanden’ zijn de toenames ten opzichte van 2004 tien procent en meer. T.o.v. 1987 zijn verschuivingen spectaculair.

Hoe men de vergelijkende resultaten sinds 1987 op de verschillende domeinen waardeert, hangt in hoge mate af van de waarde die men aan cijferen in vergelijking met getalinzicht, hoofdrekenen, schattend rekenen, procentrekenen en het kunnen maken van toepassingen met gebruik van de rekenmachine wenst toe te kennen.

3. Individuele peilingen 1987 – 2004

We beschikken over de scores van een aantal gemeenschappelijke opgaven van individuele, mondelinge toetsafnamen in de periodieke Cito-peilingen uit 1987 en 2004 die bij ongeveer 140 leerlingen zijn afgenomen.

De proefpersonen uit deze individuele peiling van 2004 zijn als volgt via een steekproef van een steekproef geselecteerd:

Op ongeveer de helft van de 122 scholen vonden er in de namiddag bij enkele leerlingen (ongeveer zes per groep) individuele afnames van vijf of zes rekenopgaven plaats. De leerlingen werden op evenredige afstand uit een alfabetisch gerangschikte leerlingenlijst geselecteerd. De individuele afnames waren erop gericht enig inzicht te krijgen in en te kunnen rapporteren over de oplossingsprocedures die de leerlingen bij het maken van de opgaven gebruiken.

De opgaven kunnen model staan voor het rekenonderdeel dat ze representeren. Ze hebben betrekking op getalinzicht, hoofdrekenen, schattend rekenen, breuken, verhoudingen en procenten.

Aangezien de steekproef van de individuele peiling te klein is, kan aan de goedscores van de betreffende opgaven geen absolute waarde worden toegekend. Maar een indicatie van de vergelijkende prestaties uit 1987 en 2004 geven ze wel. Zeker zo belangrijk zijn echter de verschillen in de wijze waarop de problemen worden opgelost.

De eerste twee opgaven van de individuele afnames dienen uit het hoofd berekend te worden…

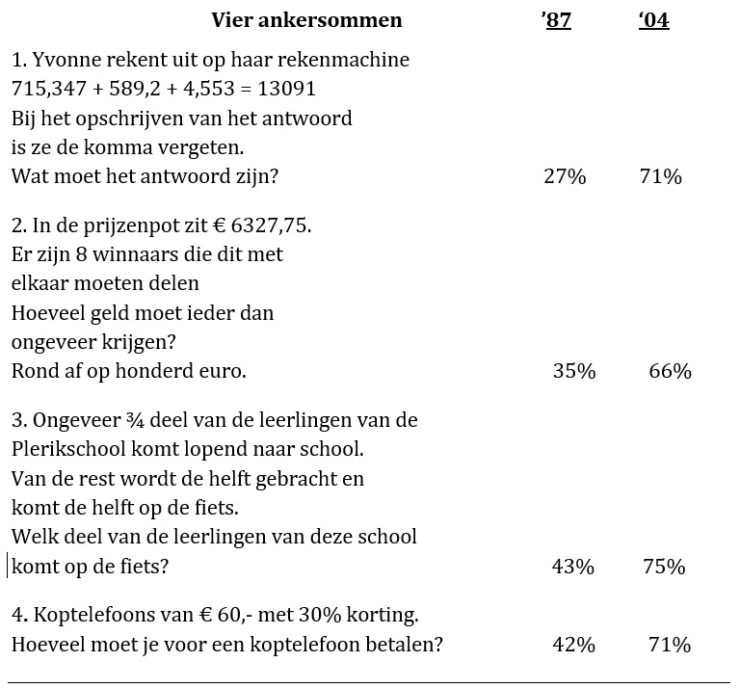
Ad. 1). In 1987 gaf 36% van de leerlingen bij de Yvonne-som het antwoord 13,091 omdat de meeste getallen drie cijfers achter de komma hebben, en kwam 6% tot 0,0013091 door het aantal cijfers achter de komma bij elkaar op te tellen; 13% rekende globaal schattend volgens 700 + 600 om de komma goed te kunnen plaatsen.

In 2004 redeneert slechts één op de tien leerlingen vormelijk via het tellen van de cijfers achter de komma’s; 55% van de kinderen rekent globaal met ronde getallen.

De Cito-onderzoekers noemen de toename van het percentage goede antwoorden ‘opzienbarend’. Maar nog opmerkelijker is wellicht het hoge percentage komma-tellers dat zich in 1987 door irrelevante vormkenmerken liet (mis)leiden.

Ad. 2). Ook de prijzenpot-som geeft een grote toename van de goedscore te zien. En weer springt de afname van het cijferend rekenen uit het hoofd en de toename van het globale rekenen in het oog. In 1987 rekende 27% van de leerlingen via 6400 : 8, terwijl in 2004 maar liefst 58% zo handig rekent. ‘Hoofdcijferen’ neemt in deze periode af van 36% naar 16%.

Ad. 3). In 1987 rekende 46% kort en goed volgens ‘de rest is ¼ en daarvan is de helft 1/8. Van de leerlingen volstond 16% met de berekening van de rest en 11% gaf de helft als antwoord.

In 2004 volgt maar liefst 81% de eerste oplossingsprocedure, zij het in vele varianten waarbij gebruik wordt gemaakt van visualiseringen (cirkel en strook) en omzettingen naar procenten en kommagetallen. De forse stijging van de goedscore is hiermee te verklaren, want in bijna alle gevallen zijn de leerlingen daarbij succesvol..

Ad. 4) In 1987 rekende 7% van de leerlingen via ‘10% is € 6, dus 30% is € 18, dus …’ In 2004 volgt 65% deze werkwijze! Dan worden ook minder begripsfouten gemaakt zoals: ’€ 60 – € 30’, en ‘30% is 1/3 deel is dus € 20’.

In het Cito-rapport wordt het volgende over deze som opgemerkt:

‘Op basis van deze resultaten kunnen we concluderen dat leerlingen meer inzicht in procenten hebben gekregen. Niet alleen maken veel meer leerlingen procentopgaven, zoals de hiervoor besproken individueel afgenomen opgaven, goed in 2004, maar ook veel meer leerlingen gebruiken in 2004 in vergelijking met 1987 oplossingsprocedures waarmee ze op een efficiëntere manier tot de oplossing komen.’

Conclusie. In deze vier voorbeelden van de individuele peiling valt op hoezeer het handige, globale en inzichtelijke rekenen in de periode 1987 – 2004 zijn toegenomen, en daarmee ook de goedscores.

Literatuur

>Beusekom, N. van, e.a. (1990/2010). Pluspunt. Den Bosch: Malmberg.

>Huitema, S., e.a. (1981/2010). De Wereld in Getallen. Den Bosch: Malmberg.

>Janssen, J., F. van der Schoot, B. Hemkes & N. Verhelst (1999). Balans van het reken-wiskundeonderwijs aan het einde van de basisschool 3. Arnhem: Cito.

>Janssen, J., F. van der Schoot & B. Hemkes (2006). Balans van het reken-wiskundeonderwijs aan het einde van de basisschool 4. Arnhem: Cito.

>Scheltens, F., B. Hemker & J. Vermeulen (2013). Balans van het reken-wiskundeonderwijs aan het einde van de basisschool 5. Arnhem: Cito.

>Treffers, A. (2015). Weg van het cijferen. Rekenmethodes vanaf 1800 tot heden. Freudenthal Group, Universiteit Utrecht. reni.casoli@gmail.com

adri.treffers@gmail.com