Over ontdekkend leren (1) – Tussen exploratie en explicatie

Adri Treffers –

De waarde van ontdekkend leren en probleem-oplossen wordt door pleitbezorgers van de Cognitive Load Theory (CLT) niet hoog ingeschat – integendeel. Zo rekent Kirschner deze kernactiviteiten van het constructivisme zelfs tot twee van de tien didactische hoofdzonden.

‘Tijdens ontdekkend leren moeten zij steeds op zoek naar verbanden tussen zaken en de principes die van kracht zijn in het domein. Maar beginners hebben nauwelijks domeinkennis en geen systematische aanpak om te onderzoeken en experimenteren. (…). Daarnaast drijft deze aanpak op de gedachte dat het kind een soort kleine wetenschapper is.’ (Kirschner et al., 2018, p. 157)

‘Laat ze eerst leren, dan begeleid oefenen, dan vrij oefenen, en misschien pas daarna zelf ontdekken’, zo vat Kirschner zijn standpunt over ontdekkend leren in een onderwijsblog samen.

Het fundamentele belang van kennis, vaardigheden en begrippen kan nauwelijks overschat worden – daar valt niet over te twisten. Maar dat leren in de CLT wordt losgekoppeld van probleem-oplossen, is echter wel vatbaar voor kritiek. Want probleem-oplossen blijkt, naast een doel op zich, ook als een didactisch middel te kunnen fungeren. Maar dan wel binnen een interactieve setting onder passende begeleiding van de leraar, zo wijst 150 jaar onderwijs met op inzicht gerichte rekenmethodes uit.

In een onderwijsblog laat Kirschner onder meer met het volgende voorbeeld zien hoe de CLT-aanpak in het rekenonderwijs uitgewerkt kan worden – een voorbeeld dat nota bene ook door voorstanders van begeleid ontdekkend leren gebruikt kan worden om aan te tonen dat probleem-oplossen aan de basis van het leren van rekenprocedures kan staan. (Treffers, 2019)

12,9 : 3 = …

Stap 1. Splits het eerste getal in helen en tienden.

12,9 splits je in 12 en 0,9

Stap 2. Deel de getallen door het tweede getal.

12 : 3 = 4  |  0,9 : 3 = 0,3

Stap 3. Tel de twee uitkomsten op.

4 + 0,3 = 4,3

Stap 4. Noteer het antwoord.

12,9 : 3 = 4,3

Een voorbeeldig probleem om leerlingen van groep 7 voor te leggen.

Ze kunnen dan opmerken dat dit stappenplan bij ‘13,5 : 3’ niet werkt, dus fout is, en daarna samen een goed stappenplan ontwikkelen van een rekenregel voor de nieuwe leerstof van ‘kommagetal gedeeld door heel getal’, onder minimale begeleiding van de leraar.

Is dit geen indicatie dat ‘beginnelingen’ minder onwetend zijn dan experts denken en experts wat minder wetend dan we zelf menen?

Nu twee voorbeelden van probleem-oplossen als doel op zich.

Neem om te beginnen het volgende vermakelijke vraagstuk.

Iemand koopt een pen voor 1 euro, verkoopt hem voor 2 euro,

koopt hem terug voor 3 euro, en verkoopt die pen voor 4 euro.

Hoeveel is de winst?

De goedscores van leerlingen van groep 7 en van geschoolde volwassenen zijn hierbij ongeveer gelijk, namelijk rond de 50 procent. En de bijpassende redeneringen van de goede en foute oplossingen verschillen evenmin. (Burns, 1987)

Hetzelfde geldt voor de volgende hilarische som:

Iemand koopt een hoedje van papier voor 1 euro en betaalt

met een munt van 2 euro. De winkelier kan niet wisselen.

Hij gaat naar zijn collega en wisselt de 2-euromunt.

De koper vertrekt met het hoedje en de 1 euro wisselgeld.

De 2 euromunt waarmee hij betaalde bleek echter vals.

De winkelier moest de boze collega die 2 euro vergoeden.

Hoeveel euro verlies heeft de winkelier al met al geleden?

Marilyn Burns beschrijft hoe je met dergelijke problemen interactief onderwijs kunt geven. De kinderen die hetzelfde antwoord hebben, gaan in groepjes staan. In ieder van de twee of drie groepjes licht een leerling het antwoord van de betreffende groep toe. Als je je laat overtuigen dat je fout zat, stap je over naar de ‘goede’ groep. En zo na een korte discussie nog een keer of meer. Daarna wordt de probleemsituatie uitgespeeld. Tot slot beschrijft ieder kind in een korte reflectie hoe zijn oplossingsproces is verlopen en waardoor het al niet van gedachten veranderde. Interactief probleemgericht onderwijs in optima forma, en naadloos passend bij de algemene doelstellingen van het rekenwiskunde-onderwijs i.c. de persoonlijke, sociale en vakspecifieke waarden. (Menne,2001; Veltman, 1999)

In een volgend blog zullen we met een modelvoorbeeld van een lettersom andermaal aantonen dat de genoemde reserve ten aanzien van ontdekkend leren onterecht is, en dat een leerstellige uitspraak over de beperkte denkkracht van kinderen, die essentieel van het denkvermogen van de expert zou verschillen, discutabel is.

De volgende eigen producties van zo’n lettersom – waarin gelijke letters voor gelijke cijfers staan, en verschillende letters voor verschillende cijfers – staan tweetalig op de ‘tegel’ met de toepasselijke tekst:

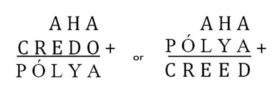
Een opgave van twee termen, met tien verschillende letters en een sprekend motto voor ‘ontdekkend leren’ – een verborgen cijfersom over Pólya, de beroemde promotor van interactief, ontdekkend wiskundeonderwijs tussen de uitersten van exploratie en explicatie.

Referenties

Burns, M. (1987). Collection of math lessons from grade 3 through 8. New York. Cuisenaire Compagny.

Kirschner, P. A., L. Claessens & S. Raaijmakers ( 2018). Op de schouders van reuzen. Meppel, Ten Brink.

Menne, J. J. M. (2001). Met sprongen vooruit. Een productief oefenprogramma voor zwakke rekenaars in het getallengebied tot100 – een onderwijsexperiment (diss.). Utrecht, Freudenthal Instituut.

Treffers, A. (2019). Leren rekenen zonder problemen? Directe instructie met uitgewerkte voorbeelden. Volgens Bartjens, 38, 4, 4-9.

Veltman, A. (1999). De restaurantles. In: Talteam, Jonge kinderen leren rekenen, 40-41. Groningen, Wolters Noordhoff.

adri.treffers@gmail.com